Home
BackFixed-fixed beam - Couple moment Mo at any point Calculator
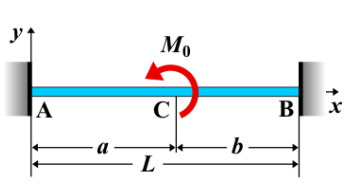
Formula
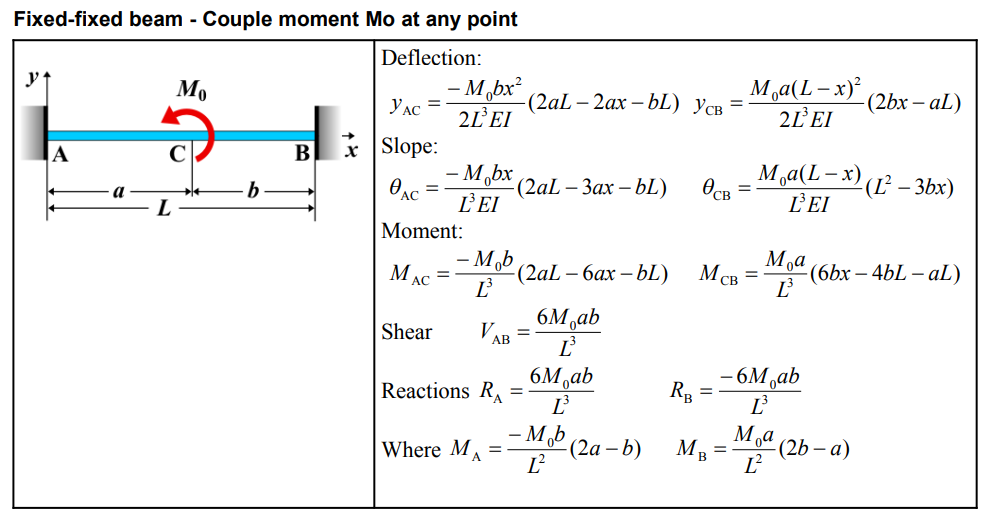
| Parameter | Formula |
|---|---|
| Deflection (AC) | \( y_{AC} = \frac{-M_0 b x^2}{2 L^3 EI} (2aL - 2ax - bL) \) |
| Deflection (CB) | \( y_{CB} = \frac{M_0 a (L - x)^2}{2 L^3 EI} (2bx - aL) \) |
| Slope (AC) | \( \theta_{AC} = \frac{-M_0 b x}{L^3 EI} (2aL - 3ax - bL) \) |
| Slope (CB) | \( \theta_{CB} = \frac{M_0 a (L - x)}{L^3 EI} (L^2 - 3bx) \) |
| Moment (AC) | \( M_{AC} = \frac{-M_0 b}{L^3} (2aL - 6ax - bL) \) |
| Moment (CB) | \( M_{CB} = \frac{M_0 a}{L^3} (6bx - 4bL - aL) \) |
| Shear | \( V_{AB} = \frac{6M_0 ab}{L^3} \) |
| Reactions (RA) | \( R_A = \frac{6M_0 ab}{L^3} \) |
| Reactions (RB) | \( R_B = \frac{-6M_0 ab}{L^3} \) |
| Where (MA) | \( M_A = \frac{-M_0 b}{L^2} (2a - b) \) |
| Where (MB) | \( M_B = \frac{M_0 a}{L^2} (2b - a) \) |
Definitions
| Symbol | Physical quantity | Units |
|---|---|---|
| E·I | Flexural rigidity | N·m², Pa·m⁴ |
| y | Deflection or deformation | m |
| θ | Slope, Angle of rotation | - |
| x | Distance from support (origin) | m |
| L | Length of beam (without overhang) | m |
| M | Moment, Bending moment, Couple moment applied | N·m |
| P | Concentrated load, Point load, Concentrated force | N |
| w | Distributed load, Load per unit length | N/m |
| R | Reaction load, reaction force | N |
| V | Shear force, shear | N |