Home
BackFixed-fixed beam - Uniformly distributed load Calculator
Formula
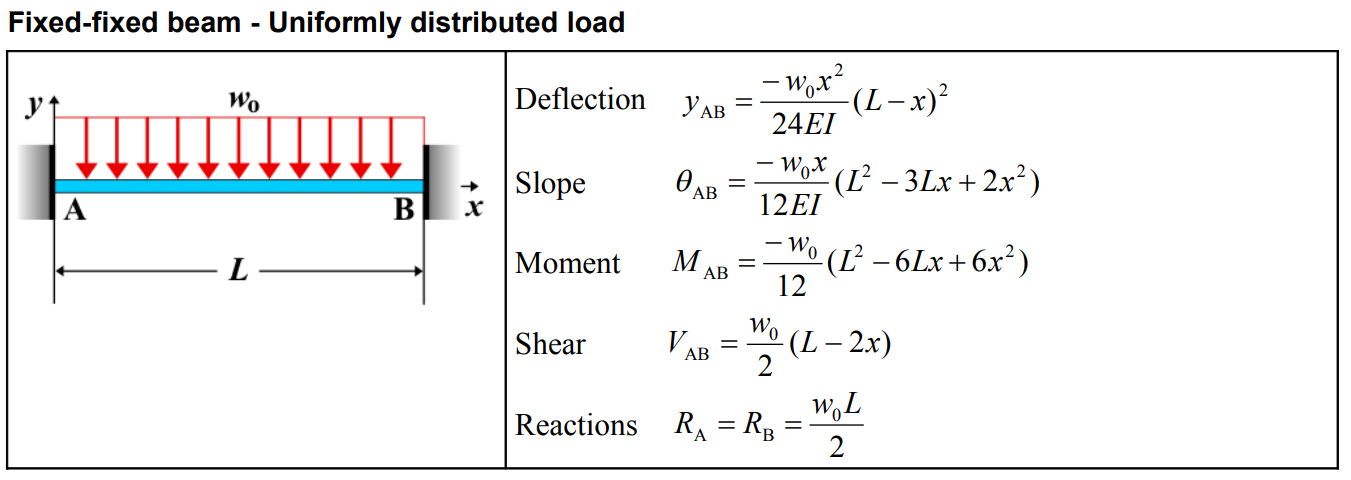
| Quantity | Formula |
|---|---|
| Deflection \(y_{AB}\) | \[ y_{AB} = \frac{-w_0 x^2 (L - x)^2}{24EI} \] |
| Slope \(\theta_{AB}\) | \[ \theta_{AB} = \frac{-w_0 x}{12EI} \left( L^2 - 3Lx + 2x^2 \right) \] |
| Moment \(M_{AB}\) | \[ M_{AB} = \frac{-w_0}{12} \left( L^2 - 6Lx + 6x^2 \right) \] |
| Shear \(V_{AB}\) | \[ V_{AB} = \frac{w_0}{2} \left( L - 2x \right) \] |
| Reactions \(R_A\) and \(R_B\) | \[ R_A = R_B = \frac{w_0 L}{2} \] |
Definitions
| Symbol | Physical quantity | Units |
|---|---|---|
| E·I | Flexural rigidity | N·m², Pa·m⁴ |
| y | Deflection or deformation | m |
| θ | Slope, Angle of rotation | - |
| x | Distance from support (origin) | m |
| L | Length of beam (without overhang) | m |
| M | Moment, Bending moment, Couple moment applied | N·m |
| P | Concentrated load, Point load, Concentrated force | N |
| w | Distributed load, Load per unit length | N/m |
| R | Reaction load, reaction force | N |
| V | Shear force, shear | N |