| Deflection (\(y_{AC}\)) |
\(y_{AC} = \frac{Px^2}{12EI L^2} [(3a^2 - 3aL - 2L^2)(L-x) + 2L(3a^2 - 3aL + L^2)]\) |
| Deflection (\(y_{CD}\)) |
\(y_{CD} = \frac{-Pa(3(L-a)(L-x)^3 - 6L^2(L-x)^2)}{12EI L^2 a^2} + \frac{-Pa[3L^2(L+a)(L-x) - 2L^2 a]}{12EI L^2}\) |
| Deflection (\(y_{DB}\)) |
\(y_{DB} = \frac{-P(L-x)}{12EI L^2} [(3aL - 3a^2 - 2L^2)(L-x)^2 + 3aL^2(L-a)]\) |
| Slope (\(\theta_{AC}\)) |
\(\theta_{AC} = \frac{Px}{12EI L^2} [(3a^2 - 3aL - 2L^2)(2L - 3x) + 4L(3a^2 - 3aL + L^2)]\) |
| Slope (\(\theta_{CD}\)) |
\(\theta_{CD} = \frac{-Pa}{4EI L^2} [-3(L-a)(L-x)^2 + 4L^2(L-x) - L^2(L+a)]\) |
| Slope (\(\theta_{DB}\)) |
\(\theta_{DB} = \frac{P}{4EI L^2} [(3aL - 3a^2 - 2L^2)(L-x)^2 + aL^2(L-a)]\) |
| Moment (\(M_{AC}\)) |
\(M_{AC} = \frac{P}{2L^2} [3a^2 L - 3aL^2 + x(2L^2 + 3aL - 3a^2)]\) |
| Moment (\(M_{CD}\)) |
\(M_{CD} = \frac{-Pa}{2L^2} [3(L-a)(L-x) - 2L^2]\) |
| Moment (\(M_{DB}\)) |
\(M_{DB} = \frac{-P(L-x)}{2L^2} [3aL - 3a^2 - 2L^2]\) |
| Shear (\(V_{AC}\)) |
\(V_{AC} = \frac{P}{2L^2} (2L^2 + 3aL - 3a^2)\) |
| Shear (\(V_{CD}\)) |
\(V_{CD} = \frac{3Pa(L-a)}{2L^2}\) |
| Shear (\(V_{DB}\)) |
\(V_{DB} = \frac{P}{2L^2} (3aL - 3a^2 - 2L^2)\) |
| Reaction (\(R_A\)) |
\(R_A = \frac{P}{2L^2} (2L^2 + 3aL - 3a^2)\) |
| Reaction (\(R_B\)) |
\(R_B = \frac{P}{2L^2} (3a^2 + 2L^2 - 3aL)\) |
| Deflection (\(y_{AC}\)) - New |
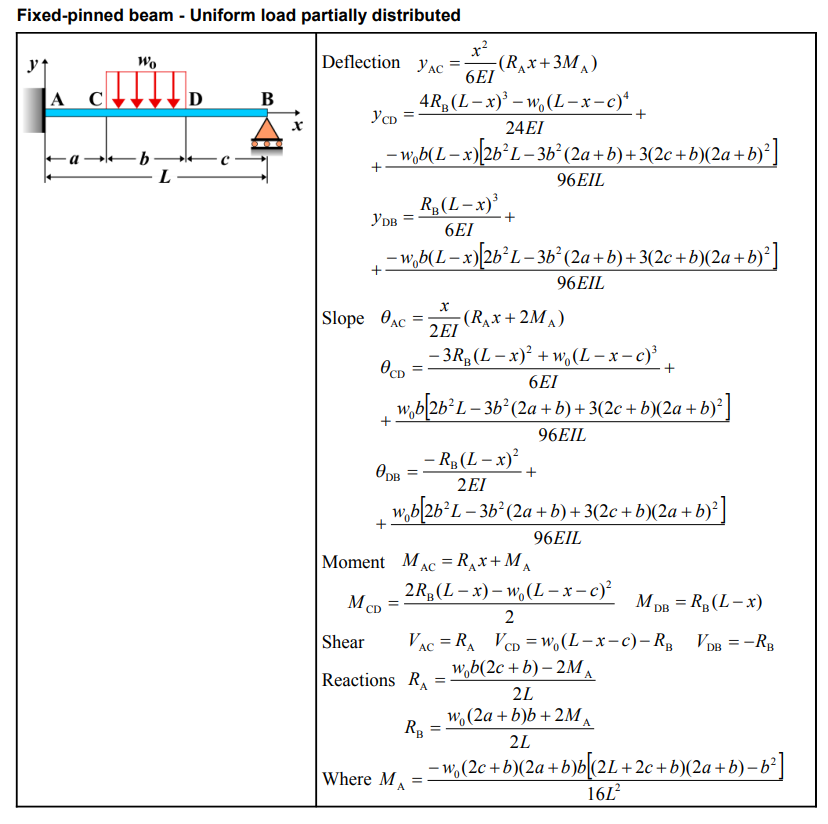
\(y_{AC} = \frac{x^2}{6EI} (R_A x + 3M_A)\) |
| Deflection (\(y_{CD}\)) - New |
\(y_{CD} = \frac{4R_B(L-x)^3 - w_0(L-x-c)^4}{24EI} + \frac{-w_0 b(L-x)[2b^2 L - 3b^2(2a+t)]}{96EI L}\) |
| Deflection (\(y_{DB}\)) - New |
\(y_{DB} = \frac{R_B(L-x)^3}{6EI} + \frac{-w_0 b(L-x)[2b^2 L - 3b^2(2a+b) + 3(2c+b)(2a+b)^2]}{96EI L}\) |
| Slope (\(\theta_{AC}\)) - New |
\(\theta_{AC} = \frac{x}{2EI} (R_A x + 2M_A)\) |
| Slope (\(\theta_{CD}\)) - New |
\(\theta_{CD} = \frac{-3R_B(L-x)^2 + w_0(L-x-c)^3}{6EI} + \frac{w_0 b[2b^2 L - 3b^2(2a+b) + 3(2c+b)(2a+b)^2]}{96EI L}\) |
| Moment (\(M_{AC}\)) - New |
\(M_{AC} = \frac{w_0 b|2b^2 L - 3b^2(2a+b)}{nt} + R x + M_A\) |
| Shear (\(V_{AC}\)) - New |
\(V_{AC} = R_A\) |
| Shear (\(V_{CD}\)) - New |
\(V_{CD} = w_0 (L-x-c) - R_B\) |
| Shear (\(V_{DB}\)) - New |
\(V_{DB} = -R_B\) |
| Reaction (\(R_A\)) - New |
\(R_A = \frac{w_0 b(2c+b) - 2M_A}{2L}\) |
| Reaction (\(R_B\)) - New |
\(R_B = \frac{w_0(2a+b)b + 2M_A}{2L}\) |

 Home
Home Back
Back