Home
BackSimple beam - Concentrated load at any point Calculator
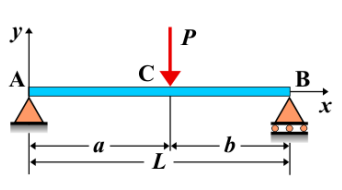
Formula
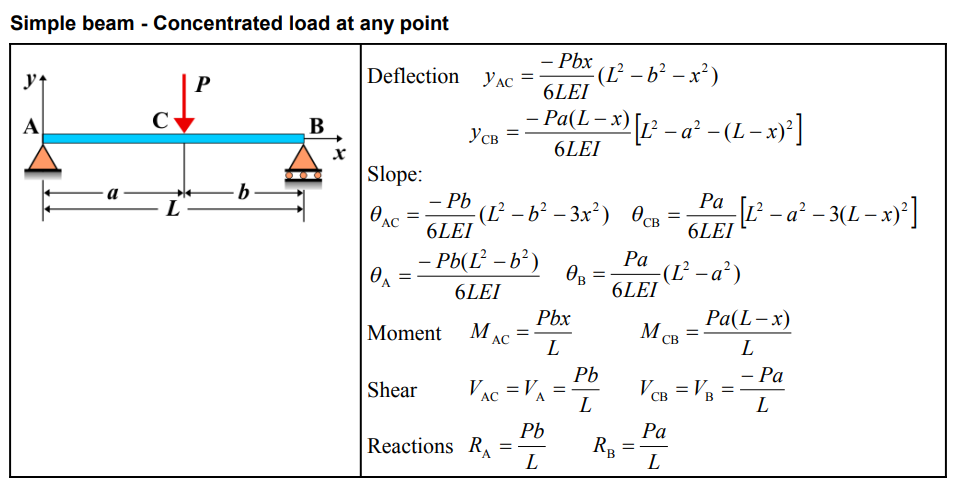
| Deflection (AC) | \( y_{\mathrm{AC}} = \frac{-Pbx}{6LEI}(L^{2}-b^{2}-x^{2}) \) |
| Deflection (CB) | \( y_{\mathrm{CB}} = \frac{-Pa(L-x)}{6LEI}\left[L^{2}-a^{2}-(L-x)^{2}\right] \) |
| Slope (AC) | \( \theta_{\mathrm{AC}} = \frac{-Pb}{6LEI}(L^{2}-b^{2}-3x^{2}) \) |
| Slope (CB) | \( \theta_{\mathrm{CB}} = \frac{Pa}{6LEI}\left[L^{2}-a^{2}-3(L-x)^{2}\right] \) |
| Slope at A | \( \theta_{\mathrm{A}} = \frac{-Pb(L^{2}-b^{2})}{6LEI} \) |
| Slope at B | \( \theta_{\mathrm{B}} = \frac{Pa}{6LEI}(L^{2}-a^{2}) \) |
| Moment (AC) | \( M_{\mathrm{AC}} = \frac{Pbx}{L} \) |
| Moment (CB) | \( M_{\mathrm{CB}} = \frac{Pa(L-x)}{L} \) |
| Shear (AC) | \( V_{\mathrm{AC}} = V_{\mathrm{A}} = \frac{Pb}{L} \) |
| Shear (CB) | \( V_{\mathrm{CB}} = V_{\mathrm{B}} = \frac{-Pa}{L} \) |
| Reactions (A) | \( R_{_A} = \frac{Pb}{L} \) |
| Reactions (B) | \( R_{_B} = \frac{Pa}{L} \) |