Home
BackSimple beam - Sinusoidal distributed load Calculator
Formula
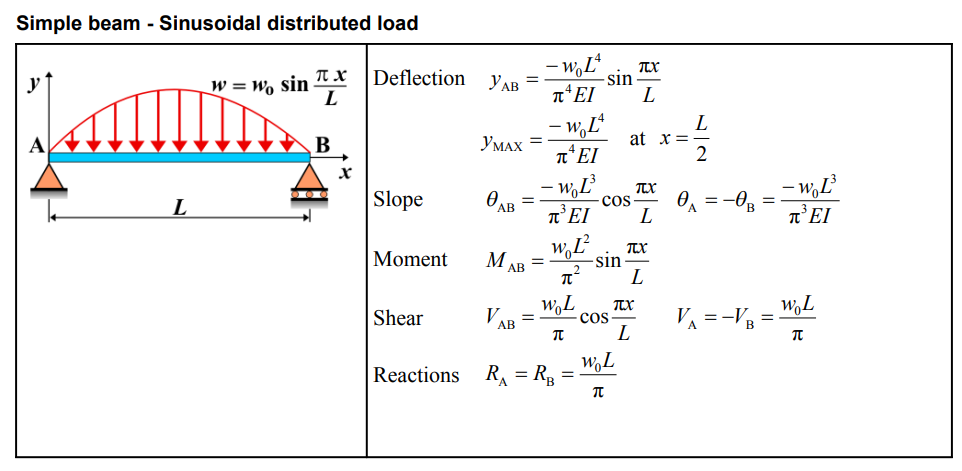
| Category | Formula |
|---|---|
| Deflection \( y_{AB} \) | \[ y_{AB} = \frac{-w_{0}L^4}{\pi^4EI} \sin \frac{\pi x}{L} \] |
| Deflection at \( x = \frac{L}{2} \) | \[ y_{MAx} = \frac{-w_{0}L^4}{\pi^4EI} \quad \text{at } x = \frac{L}{2} \] |
| Slope \( \theta_{AB} \) | \[ \theta_{AB} = \frac{-w_{0}L^3}{\pi^3EI} \cos \frac{\pi x}{L} \] |
| Slope at Ends | \[ \theta_{A} = -\theta_{B} = \frac{-w_{0}L^3}{\pi^3EI} \] |
| Moment \( M_{AB} \) | \[ M_{AB} = \frac{w_{0}L^2}{\pi^2} \sin \frac{\pi x}{L} \] |
| Shear \( V_{AB} \) | \[ V_{AB} = \frac{w_{0}L}{\pi} \cos \frac{\pi x}{L} \] |
| Shear at Ends | \[ V_{A} = -V_{B} = \frac{w_{0}L}{\pi} \] |
| Reactions \( R_{A}, R_{B} \) | \[ R_{A} = R_{B} = \frac{w_{0}L}{\pi} \] |
Definitions
| Symbol | Physical quantity | Units |
|---|---|---|
| E·I | Flexural rigidity | N·m², Pa·m⁴ |
| y | Deflection or deformation | m |
| θ | Slope, Angle of rotation | - |
| x | Distance from support (origin) | m |
| L | Length of beam (without overhang) | m |
| M | Moment, Bending moment, Couple moment applied | N·m |
| P | Concentrated load, Point load, Concentrated force | N |
| w | Distributed load, Load per unit length | N/m |
| R | Reaction load, reaction force | N |
| V | Shear force, shear | N |